Cor Zwanenburg1, Antonis Mavritsakis2, Britt Wittekoek2, Etienne Alderlieste2
1 Deltares, TUDelft, Delft, Nederland
2 Deltares, Delft, Nederland
ABSTRACT
De mogelijkheden van numerieke methoden in de geotechniek zijn de afgelopen jaren enorm toegenomen. Deze toename faciliteert de maatschappelijke wens om hogere eisen te stellen aan civiel technische constructies, zoals bijvoorbeeld de toelaatbare faalkans van waterkeringen of de beïnvloeding van bestaande bebouwing in stedelijk gebied. Het succesvol toepassen van numerieke methoden begint bij het valideren van de methoden. Hiervoor is betrouwbare meetdata nodig. Veldmetingen kunnen hierin slechts in beperkte mate voorzien, met name wanneer het gaat om het valideren van bezwijkgedrag. In de Geocentrifuge kunnen relatief eenvoudig series (bezwijk)proeven worden uitgevoerd en zo de benodigde meetdata worden verkregen. De validatie kan worden uitgevoerd door een directe vergelijking te maken tussen meetdata en voorspelling. Echter, met behulp van een Bayesiaanse analyse kan meer informatie uit de vergelijking worden gehaald en kan bijvoorbeeld worden aangegeven wat de bijdrage is van heterogeniteit in de ondergrond aan het verschil tussen de metingen en de berekeningen. De modelfactor kan dan worden afgeleid met een verwachtingswaarde en een onzekerheidsmarge.
KERNWOORDEN
Geocentrifuge, Numerieke modellen, Geo statistiek
Inleiding
In de afgelopen decennia zijn de eisen die vanuit het maatschappelijk belang aan civiel technische constructies worden gesteld geleidelijk aan strenger geworden. Voorbeelden hiervan zijn veiligheid tegen overstromen en de invloed die bouwactiviteiten in stedelijk gebied hebben op hun omgeving. Als gevolg van de verwachte zeespiegelstijging en toenemende verstedelijking mag verwacht worden dat deze trend in de komende jaren zal doorzetten. Door recente numerieke ontwikkelingen wordt het eenvoudiger geavanceerde ontwerpberekeningen uit te voeren. Echter, om de gevraagde hoge eisen waar te kunnen maken dienen de ontwerpberekeningen in voldoende mate nauwkeurig te zijn. Hiervoor is validatie met meetdata noodzakelijk. Het probleem dat zich hierbij voordoet is dat het verzamelen van betrouwbare meetdata van geotechnische constructies niet eenvoudig is. Zo is relevante meetdata van bezwijkgedrag slechts beperkt voor handen. Maar ook het vervormingsgedrag van de ondergrond is niet eenvoudig eenduidig vast te leggen. Het uitvoeren van modelproeven kan hier een oplossing bieden. Omdat grondgedrag sterk spanningsafhankelijk is, is voor geotechnische schaalmodellen het gebruik van de Geocentrifuge onvermijdelijk. In de Geocentrifuge, zie figuur 1, wordt de centrifugaalkracht gebruikt om de zwaartekracht te verschalen. Zo kan, tijdens de uitvoering van de proef, de spanningen in het model in overeenstemming worden gebracht met de spanningen van een vergelijkbare geotechnische constructie op ware grootte. Hierdoor vertoont het model hetzelfde grondgedrag als de werkelijkheid wordt gevonden.

Dit artikel beschrijft een voorbeeld van geotechnisch onderzoek in de Geocentrifuge met als doel validatie van numerieke methoden. De validatie bestaat niet alleen uit de deterministische vergelijking tussen de meetdata en de numerieke simulatie, maar beschrijft tevens op hoofdlijnen hoe aan de hand van Bayesiaanse statistiek een modelfactor en de bijbehorende onzekerheidsmarge kan worden afgeleid. Op deze wijze fungeert de Geocentrifuge als een testbank voor numerieke modellen.
Het onderzoek, de plaatdrukproef
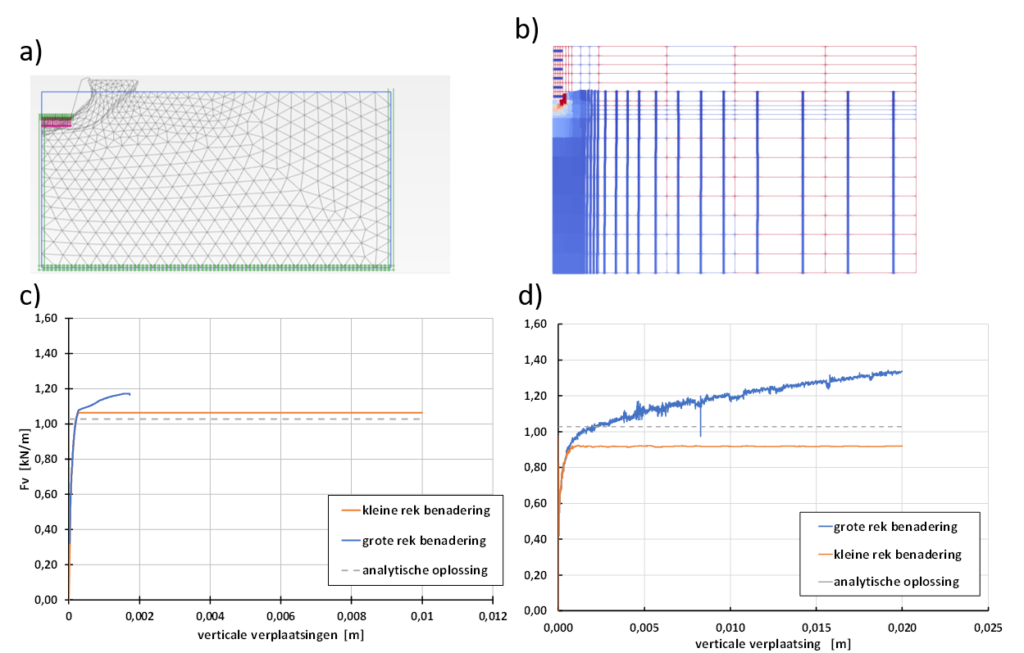
Als illustratie hoe de Geocentrifuge kan worden ingezet als testbank voor numerieke modellen wordt een serie modelproeven uitgevoerd waarin een plaatdrukproef wordt gesimuleerd. Voor het berekenen van de druk die nodig is om een bepaalde verplaatsing te realiseren zijn verschillende analytische oplossingen beschikbaar en veel numerieke simulaties gepubliceerd. Dit geldt met name wanneer de kracht die nodig is om de plaat weg te drukken wordt vergeleken met het berekenen van de funderingsdruk van een fundering op staal (o.a. Das, 2017; van Baars, 2018). Deze oplossingen gaan echter uit van een kleine rekbenadering. Voor relatief kleine vervormingen, die bijvoorbeeld optreden bij het begin van bezwijken van een plaatfundering op een stijve ondergrond, levert de kleine rekbenadering betrouwbare resultaten op. Echter, bij grote vervormingen ontstaan er afwijkingen (Teunissen & Zwanenburg, 2017). Bij het wegdrukken van de plaat zal de maximale druk toenemen. Dit wordt onder andere verklaard door de toenemende dekking, het gewicht van de grond dat zich tussen de plaat en het maaiveld bevindt. De dekking neemt niet alleen toe omdat de plaat onder het maaiveld wordt gedrukt, maar ook door vervorming van de grond naast de plaat waardoor het maaiveld wordt opgedrukt. Hiermee ontstaat er een verband tussen de sterkte, de maximale druk enerzijds en de stijfheid van de grond, die bepalend is voor de maaiveldstijging anderzijds. De bijdrage van de verandering in geometrie wordt aangeduid met geometrische niet-lineariteiten en wordt in de conventionele analytische oplossing niet in beschouwing genomen. Geometrische niet-lineariteiten worden eveneens gevonden bij beperkte laagdikte. Hierbij wordt de vorming van het bezwijkmechanisme beperkt door de beperkte laagdikte en draagt de beperkte laagdikte bij aan de ondervonden weerstand. Er zijn verschillende numerieke methoden beschikbaar om grote rek analyses, waarmee dergelijke geometrische niet-lineariteiten kunnen worden gesimuleerd, uit te kunnen voeren. Zo zijn onder andere updated mesh technieken in een eindig elementen omgeving beschikbaar of kan met de Material Point Method, MPM berekeningen worden uitgevoerd. Omdat de analytische oplossingen uitgaan van de kleine rekbenadering en die geometrische niet-lineariteiten niet modelleren kunnen deze niet worden toegepast voor het valideren van de numerieke methoden waarmee de geometrische niet-lineariteiten wel worden gemodelleerd. In plaats daarvan wordt met behulp van de Geocentrifuge een serie proeven uitgevoerd aan de hand waarvan een validatie kan worden uitgevoerd.
Voorafgaand aan de uitvoering van de proeven is een serie numerieke berekeningen uitgevoerd om het probleem verder te verkennen en de centrifuge proef verder uit te werken. In het onderzoek ligt de nadruk op ongedraineerd gedrag van slappe grond. Opgemerkt wordt dat door uit te gaan van ongedraineerd gedrag de discussie over associatief en niet-associatief materiaal gedrag (Teunissen, 2016; van Baars, 2018) kan worden vermeden. Door uit te gaan van slappe klei worden de grote vervormingen gevonden die voor geometrische niet lineariteiten van belang zijn. Opgemerkt wordt dat voor slappe klei een punching shear mechanisme als bezwijkmechanisme zal worden gevonden (Das, 2017) en geen klassieke Prandtl wig.
Figuur 2 geeft een voorbeeld van rekenresultaten. Berekeningen zijn uitgevoerd met een kleine rek benadering en een grote rek benadering. De kleine rek benadering sluit zowel voor de eindig elementen berekening als met de MPM analyse goed aan op de analytische oplossing. Voor de grote rek benadering wordt een toenemende weerstand bij toenemende verplaatsing gevonden. Opvallend is dat de eindige elementen berekening numerieke problemen laat zien met de knooppunten die direct naast de plaat gelegen zijn. In de eindige updated mesh analyse (eindige elementen) leidt dit tot het vastlopen van de berekening reeds bij relatief kleine rekken. Oplossingen als extra sterkte aan de toplaag toekennen of een kleine belasting op het maaiveld simuleren leiden nauwelijks tot verbetering. In het verdere onderzoek wordt daarom vooral gekeken naar MPM berekeningen.
Bayesiaanse interpretatie
Traditioneel worden centrifugeproeven op deterministische wijze geïnterpreteerd. De beste schatting van grondeigenschappen wordt in een rekenmodel, hier MPM, gebruikt om het meest waarschijnlijke gedrag van de centrifugeproef te voorspellen. Bayesiaanse statistiek maakt echter ook de kwantificering van de onzekerheid in de modelvalidatie mogelijk en kunnen op probabilistisch niveau conclusies worden getrokken. Figuur 3 geeft de Bayesiaanse analyse schematisch weer. Het model legt de belangrijkste bronnen van onzekerheid die de modelfactor beïnvloeden vast. Door deze bronnen aan te pakken, wordt de reduceerbare onzekerheid die bijdraagt aan onzekerheid in de modelfactor verminderd. De niet-herleidbare onzekerheid in de modelfactor is ofwel het gevolg van bronnen die niet zijn gemodelleerd, dan wel het gevolg van de inherente onzekerheid in de gemodelleerde bronnen. Voorbeelden hiervan zijn de ruis van de laboratoriumdata, de heterogeniteit van de grond in de centrifuge dan wel in de laboratoriumproeven en de meetfout in de centrifugemetingen.
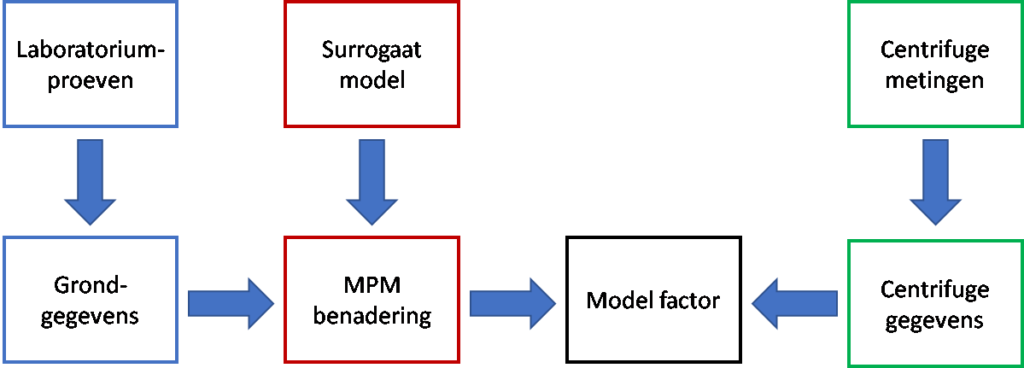
De Bayesiaanse analyse van de centrifugeproeven omvat de volgende stappen:
- Bepaling van de verdeling van de grondeigenschappen
Bayesiaanse statistiek wordt toegepast om de kansdichtheidsverdelingen voor de sterkte- en stijfheidseigenschappen van de grond af te leiden uit laboratoriumproeven. Bovendien neemt Bayesiaanse analyse voorkennis over de eigenschappen mee in de afleiding van de verdelingen. Dergelijke voorkennis kan afkomstig zijn uit databases, empirische correlaties of expert opinion. De verdeling van de grondeigenschappen kan worden gebruikt in een probabilistische analyse met het MPM-model.
- Bepalen responsverdeling van het MPM-model
Het doel van deze stap is om de doorwerking van onzekerheid in grondeigenschappen te beschrijven door een probabilistische analyse uit te voeren voor de MPM-resultaten, in het geval van de plaatdrukproef, de benodigde kracht om een bepaalde verplaatsing te realiseren. Aangezien de MPM rekenkundig veeleisend is en voor het afleiden van de responsverdeling veel berekeningen nodig zijn, wordt een surrogaatmodel gebouwd, dat een snelle benadering van de MPM-modelrespons mogelijk maakt. Ondanks zijn praktische bruikbaarheid, veroorzaakt het surrogaatmodel inherent benaderingsonzekerheid, die door de probabilistische analyse als een extra bron van onzekerheid moet worden behandeld.
- Afleiding van de modelfactor en bijbehorende verdeling
Volgens Zang et al. (2009) kan de modelfactor worden gedefinieerd als de verhouding tussen de door het model voorspelde waarde en de in de proef waargenomen waarde. In het geval van de plaatdrukproef gaat het om de verhouding van de voorspelde en gemeten druk om een bepaalde verplaatsing te realiseren. De Bayesiaanse analyse geeft de mogelijkheid om de verdeling van de modelfactor vast te stellen door de onzekerheid van het MPM-model, inclusief de onzekerheid in grondeigenschappen te combineren met het resultaat van de centrifugeproeven.
Op het moment van het schrijven van dit artikel zijn de centrifugeproeven nog in voorbereiding. Er is nog geen data beschikbaar om de modelfactor en bijbehorende onzekerheid te bepalen. In volgende artikelen zullen de resultaten worden gepresenteerd.
CONCLUSIES
In dit artikel wordt een voorbeeld uitgewerkt hoe de Geocentrifuge kan bijdragen aan het valideren van complexe rekenmodellen. Het voorbeeld betreft een plaatdrukproef waarbij met name gekeken wordt naar grote vervormingen waarvoor geometrische niet-lineariteiten een rol spelen.
De validatie zal op basis van Bayesiaanse analyse worden uitgevoerd. Dit leidt niet alleen tot de verwachtingswaarde van de modelfactor, vergelijkbaar met een deterministische benadering, maar ook tot de onzekerheid in de bepaling. Dit levert waardevolle inzichten op voor de technische praktijk en geeft de mogelijkheid voor de afleiding van de karakteristieke waarde van de modelfactor, die zou kunnen worden gebruikt om de kloof te overbruggen tussen de zeer nauwkeurige MPM-analyse en de semi-probabilistische benadering van onzekerheid die door de normen wordt gehanteerd.
BRONVERMELDING
Van Baars, S. (2018), 100 Years of Prantl’s Wedge, IOS Press, Amsterdam.
Das B.M. (2017), Shallow foundations, bearing capacity and settlement, 3rd edition, Taylor & Francis Group, Boca Raton.
Teunissen, J.A.M. (2016), Wrijving in sterkte berekeningen, Geotechniek, juli 2016, p 8-13.
Teunissen. J.A.M. & Zwanenburg, C. (2017), Modelling strains of soft soils, in proceedings of the 1st International Conference on the Material Point Method, MPM2017doi:10.1016/j.proeng.2017.01.049
Zhang, L. L., Tang, W. H., & Zhang, L. M. (2009), Bayesian model calibration using geotechnical centrifuge tests, in Journal of geotechnical and geoenvironmental engineering, 135(2), 291-299.



