Toepassing van een Data-Driven aanpak voor het bepalen van zetting
Klaas Siderius1, Harrie Wiltinge1
1 Fugro, Groningen, Nederland
ABSTRACT
Het bepalen van het zettingsgedrag van grond blootgesteld aan een spanningsverhoging is een vraagstuk wat al sinds de beginjaren van de geotechniek wordt onderzocht. In de afgelopen decennia zijn verscheidene modellen ontwikkeld waarmee het zettingsgedrag kan worden beschreven (Koppejan, NEN-Bjerrum, Isotachenmodellen etc.). Hoewel de modellen steeds beter in staat lijken te zijn om het grondgedrag realistischer te beschrijven zijn er in de praktijk nog steeds (grote) afwijkingen tussen voorspeld en gemeten zakkingsgedrag. Een alternatieve methode (CRACA) om het zettingsgedrag te bepalen waarbij data uit samendrukkingsproeven als directe input wordt gebruikt voor het bepalen van het zettingsgedrag is gepresenteerd in (Doherty & Bransby, 2019). Deze methode maakt gebruik van relatieve eenvoudige formuleringen maar heeft als voordeel een geminimaliseerde menselijke/model interpretatie. In dit artikel wordt het model toegepast op samendrukkingsproeven en proefterpen uitgevoerd bij een project en worden vergelijkingen gemaakt met een traditionele zettingsberekening.
KERNWOORDEN
Zettingsprognose, Data-Driven, CRACA, Koppejan
INTRODUCTIE
Het voorspellen van de zetting die optreedt door een belastingverhoging is een klassiek geotechnisch vraagstuk wat regelmatig voorbij komt. Karl Terzaghi was één van de eersten die een poging heeft ondernomen om met een model een voorspelling van de te verwachten zetting van een grondlaag ten gevolge van een belastingverhoging te geven. Met voortschrijdend inzicht en kennisontwikkeling zijn er verscheidene modellen van het werk van Karl Terzaghi afgeleid of zijn er nieuwe formuleringen bedacht waarmee de modellen beter in staat zijn om de werkelijkheid te benaderen. Hoewel met de komst van geavanceerdere modellen zoals NEN-Bjerrum, Fokkens, of de Isotachenmethode zetting op laboratoriumschaal beter kan worden benaderd blijven in de praktijk grote verschillen in voorspellingen onderling of de werkelijkheid aanwezig. Deze verschillen worden voornamelijk veroorzaakt door, monsterverstoring, heterogeniteit van de grond, modelfouten en verschillen in parameterafleiding. In deze paper wordt met het zettingsmodel Creep And Consolidation Analysis (CRACA) (Doherty & Bransby, 2019), waarbij direct gebruik wordt gemaakt van de meetdata van een samenddrukkingsproef de zetting ten gevolge van een belastingverhoging bepaald..
BESCHIKBARE DATA
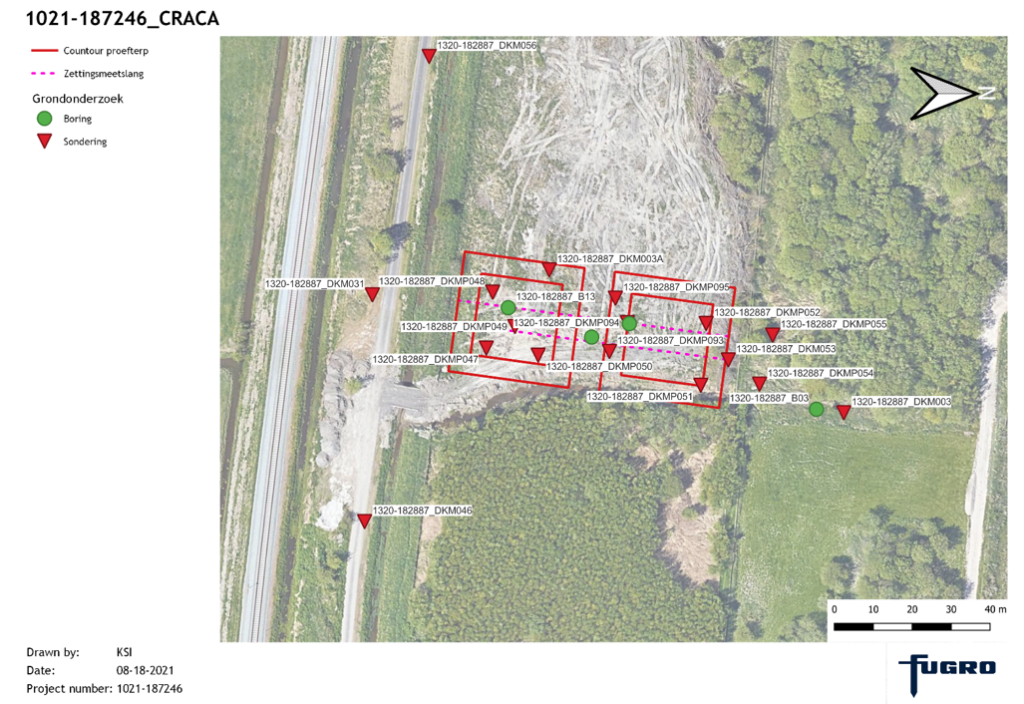
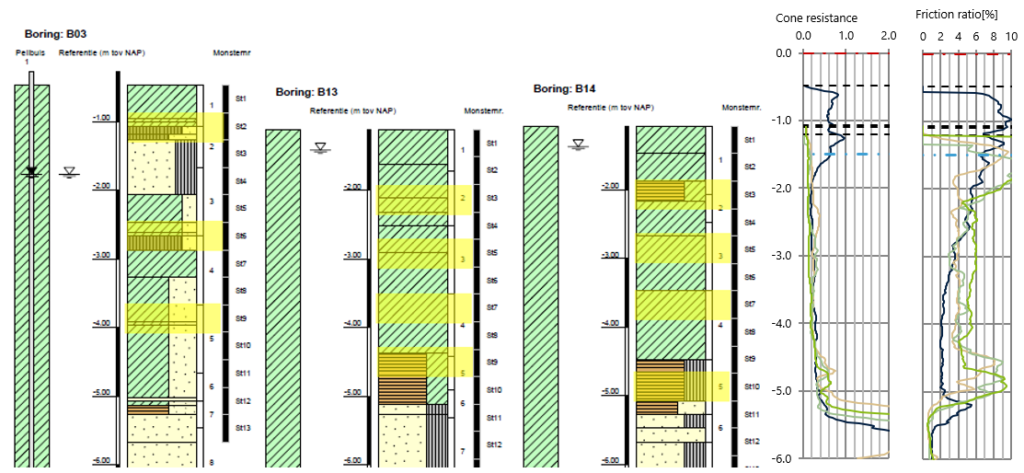
Het CRACA model wordt gebruikt voor zettingsberekeningen ten behoeve voor het bouwrijp maken van een terrein. Voor het vaststellen van bodemgesteldheid en de samendrukbaarheid van de ondergrond zijn diverse sonderingen, boringen en laboratoriumonderzoeken uitgevoerd. Ter verificatie en ondersteuning van de zettingsberekeningen zijn 2 proefterpen aangelegd waarvan de zakking wordt gemonitord. Tijdens het schrijven van deze paper zijn de proefterpen reeds aangebracht echter is de meetdata nog niet beschikbaar. De locatie van de proefterpen en het grondonderzoek is weergegeven in Figuur 1. Bij 3 boringen zijn continu monsters gestoken en zijn op geselecteerde monsters samendrukkingsproeven uitgevoerd (in totaal 11). In Figuur 2 is de proefterp tijdens aanleg te zien. In Figuur 3 is de laboratoriumclassificatie van de 3 boringen en de resultaten van nabije sonderingen weergeven. In het boorprofiel is met gele arcering de diepte van de monsterbus aangegeven waaruit monsters zijn genomen voor de samendrukkingsproeven.
De boringen en sonderingen laten een redelijke homogene bodemopbouw zien. Bij B13 en B14 is een dikker veenpakket op diepte aangetroffen en is geen zandlaag nabij de oppervlakte aangetroffen. Op basis van de classificatie en sonderingen wordt bij B13 en B14 een grotere zetting verwacht door de grotere dikte aan samendrukbare lagen.
Figuur 1; plattegrond van de proefterpen en de locatie van grondonderzoek
Figuur 2; foto van de proefterpen tijdens aanleg
Figuur 3; laboratoriumclassificatie van de boringen, diepte van de gestoken monsters (gele arcering) en nabije sonderingen
BESCHRIJVING CRACA MODEL
Het “Creep and Consoliation Analysis” model (Doherty & Bransby, 2019) is ontwikkeld om subjectiviteit in de afleiding van modelparameters uit laboratoriumdata weg te nemen. De motivatie voor het wegnemen van deze subjectiviteit is gevonden in een “blind prediction event” waarvan de resultaten zijn gepubliceerd in (Kelly, Sloan, Pineda, Kouretzis, & Huang, 2018). Bij dit event zijn grote verschillen in zettingspredicties gevonden en is de subjectiviteit bij parameterafleiding als één van de oorzaken aangemerkt. Hoewel in de Nederlandse praktijk parameterafleiding uit laboratoriumproeven sterk is gereguleerd in normen en richtlijnen kunnen ook hier verschillen ontstaan door de interpretatie van een individueel persoon (Houkes, 2016).
Het CRACA model bestaat uit 3 componenten; 1.) Consolidatie, 2.) primair compressie en 3.) secundaire compressie/kruip. In dit artikel wordt een beperkte beschrijving op hoofdlijnen gegeven voor de volledige beschrijving wordt verwezen naar (Doherty & Bransby, 2019) of de website http://www.geocalcs.com waar het model gratis beschikbaar is gesteld en als online tool kan worden gebruikt.
1.) Consolidatie
In traditionele zettingsmodellen wordt het consolidatieproces benaderd door de consolidatiecoëfficiënt . De consolidatiecoëfficiënt kan visueel worden bepaald door de methode van Cassegrande of Taylor. Vervolgens dient een keuze te worden gemaakt welke wordt gebruikt in de berekening. De is geen constante waarde maar afhankelijk van de opgetreden rek of het poriëngetal ( ), zie bijvoorbeeld (Hoefsloot, 2015). Met CRACA wordt de consolidatiecoëfficiënt voor elke belastingstap en samendrukkingsproef bepaald door het fitten van een één-dimensionaal consolidatiemodel waarmee een best-fit waarde voor wordt verkregen. Hierbij dient een keuze te worden gemaakt voor het gedeelte van de opgetreden zetting in een belastingtrap wat kan worden toegeschreven aan primaire samendrukking, een typische waarde hiervoor is 70% (Doherty & Bransby, 2019). In Tabel 1 aangeduid als Cv settlement portion.
2.) primaire compressie
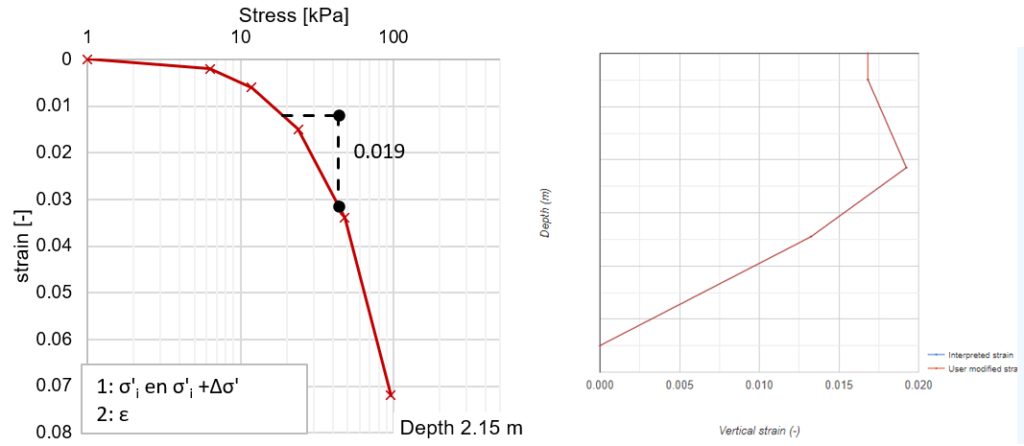
Bij traditionele zettingsmodellen worden modelparameters afgeleid die de samendrukbaarheid van de grond vertegenwoordigen, bijvoorbeeld / en / voor het Koppejan model of , en voor het isotachen model. Aanvullend zijn vaak parameters nodig zoals de grensspanning of intrinsieke tijd om onderscheid tussen maagdelijkebelasting en ontlast-herbelast gedrag. Met CRACA wordt de meetdata direct gebruikt zonder het afleiden van benaderingsparameters die de meetdata beschrijven. Het gemeten spanningspad wordt direct geïnterpoleerd om de optredende rek over een bepaald spanningsverhogingstraject en diepte te bepalen. De procedure voor het bepalen van de optredende rek in een grondlaag ten gevolge van een spanningsverhoging is visueel weergegeven in Figuur 1 links. De afgeleide rek wordt vervolgens lineair toegekend en geïnterpoleerd over de diepte van de samendrukbare lagen Figuur 1 rechts.
Figuur 4; links: visuele weergave directe bepaling rek t.g.v. spanningsverhoging in samendrukkingsproefresultaat B03-2.15m. Rechts interpolatie van de afgeleide rek over de diepte
3.) secundaire compressie / kruip
De derde component van het model bepaald de rek ten gevolge van het kruip mechanisme. De kruiprek wordt wederom direct bepaald uit de meetdata. Hierbij wordt van elke belastingtrap in een samendrukkingstrap de helling van de zettings-log(tijd) grafiek aan het einde van de belastingtrap bepaald. Deze waarde wordt op gelijke manier toegekend en lineair geïnterpoleerd over de diepte. De verschillende componenten worden bij elkaar opgeteld waarbij de primaire zetting afhankelijk is van de consolidatiegraad welke volgt uit het gefitte één-dimensionale consolidatiemodel. De kruip wordt bepaald volgens onderstaande formule
Hierin is de consolidatiegraad, de afgeleide helling, is de duur van het gedeelte van de belastingtrap dat is gebruikt voor het bepalen van .
RESULTATEN
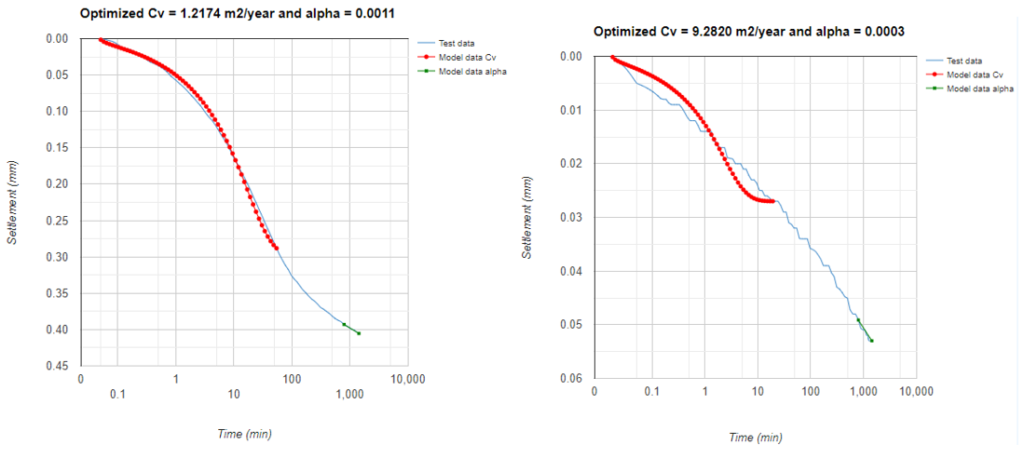
De beschikbare samendrukkingsproefresultaten voor de proefterpen zijn ingevoerd in het CRACA-model en per boring is de zetting berekend na 1 jaar en een belastingverhoging van 45 kPa. Voor alle belastingtrappen is een fit gemaakt met het één-dimensionale consolidatiemodel en is een primair en secundair rekprofiel over de diepte gemaakt. De juistheid van het consolidatiemodel om de meetdata te benaderen is variabel. Over het algemeen is de fit bij hogere belastingtrappen beter, zie Figuur 2. Aan de linkerzijde van Figuur 2 is en relatief goede fit te zien bij een belasting van 80.1 kPa. Aan de rechterzijde (belasting 10.1 kPa) is het lastiger om onderscheid te maken tussen primaire en secundaire zetting en is de fit minder goed. Voor het bepalen van de eindrek (volledige consolidatie) heeft dit geen invloed aangezien deze rechtstreeks wordt afgeleid uit de samendrukkingsproef. Een overzicht van de afgeleide parameters is gegeven in Tabel 1 en is ook de berekende zetting na 1 jaar weergegeven in de laatste kolom.
Figuur 5; fit van de consolidatiecurve (rood) en de bepaling van de kruipcomponent (groen), links een goede fit (B03-80.1kPa), rechts een minder goede fit (B13-10.1kPa)
Tabel 1; Overzicht samendrukkingsproeven en afgeleide parameters met CRACA
| Borehole ID | Depth | Soil description | Applied load | Cv settlement portion | strain incement | Cv | alpha | settlement |
| [-] | [m] | [-] | [kPa] | [-] | [-] | [m²/year] | [-] | [m] |
| B13 | 1.00 | KLEI, niet organisch, lichtgroen, stevig, zwak kalkhoudend | 7.9 | 0.5 | 0.018 | 138.3 | 0.0001 | 0.36 |
| 16.1 | 0.5 | 60.9 | 0.0003 | |||||
| 31.9 | 0.5 | 60.6 | 0.0008 | |||||
| 64.2 | 0.5 | 67.1 | 0.0012 | |||||
| 1.72 | KLEI, niet organisch, lichtgroen, stevig, zwak kalkhoudend | 10.1 | 0.5 | 0.034 | 9.3 | 0.0003 | ||
| 20 | 0.5 | 11.6 | 0.0009 | |||||
| 39.8 | 0.5 | 10.8 | 0.0018 | |||||
| 80 | 0.5 | 11.9 | 0.0031 | |||||
| 2.55 | KLEI, zwak organisch, grijs, slap, kalkhoudend | 6.8 | 0.7 | 0.063 | 1.7 | 0.0002 | ||
| 12.9 | 0.5 | 13.3 | 0.0005 | |||||
| 26.1 | 0.5 | 16.0 | 0.0013 | |||||
| 52 | 0.5 | 9.0 | 0.0051 | |||||
| 103.8 | 0.5 | 2.5 | 0.0077 | |||||
| 3.37 | VEEN, kleiig, amorf, erg dun gelaagd, donkerbruin, zeer slap, met weinig kleilensjes | 8.9 | 0.5 | 0.117 | 10.2 | 0.0007 | ||
| 18.2 | 0.5 | 10.9 | 0.0014 | |||||
| 35.8 | 0.5 | 24.9 | 0.0038 | |||||
| 71.9 | 0.5 | 4.7 | 0.0128 | |||||
| 144.1 | 0.6 | 1.5 | 0.0121 | |||||
| B14 | 0.94 | VEEN, kleiig, pseudo fijn vezelig, donkerbruin, matig slap, met veel kleibrokjes | 4.1 | 0.7 | 0.066 | 2.4 | 0.0004 | 0.24 |
| 7.9 | 0.7 | 6.6 | 0.0010 | |||||
| 15.1 | 0.5 | 7.6 | 0.0015 | |||||
| 30 | 0.5 | 9.2 | 0.0024 | |||||
| 60.3 | 0.5 | 6.0 | 0.0033 | |||||
| 1.70 | KLEI, niet organisch, groen, slap, zwak kalkhoudend | 5.1 | 0.7 | 0.018 | 53.5 | 0.0001 | ||
| 10.1 | 0.7 | 0.1 | 0.0002 | |||||
| 19.9 | 0.7 | 111.2 | 0.0002 | |||||
| 40.2 | 0.7 | 195.8 | 0.0005 | |||||
| 79.8 | 0.7 | 200.6 | 0.0007 | |||||
| 2.60 | KLEI, niet organisch, grijs, stevig, kalkloos | 6.2 | 0.7 | 0.034 | 528.8 | 0.0002 | ||
| 11.7 | 0.7 | 235.9 | 0.0003 | |||||
| 23.8 | 0.5 | 347.7 | 0.0005 | |||||
| 48 | 0.5 | 80.2 | 0.0022 | |||||
| 95.8 | 0.7 | 5.2 | 0.0044 | |||||
| 3.70 | VEEN, siltig, pseudo vezelig, erg dun gelaagd, donkergrijs, stevig | 17.8 | 0.5 | 0.035 | 157.8 | 0.0005 | ||
| 36 | 0.7 | 14.3 | 0.0015 | |||||
| 71.8 | 0.7 | 2.7 | 0.0048 | |||||
| 143.9 | 0.7 | 0.7 | 0.0119 | |||||
| B03 | 0.49 | Klei, grijs, zwak organisch, stevig, kalkloos | 5.1 | 0.7 | 0.028 | 0.3 | 0.0005 | 0.17 |
| 10 | 0.6 | 4.1 | 0.0004 | |||||
| 19.9 | 0.6 | 2.3 | 0.0006 | |||||
| 40.1 | 0.65 | 1.6 | 0.0009 | |||||
| 80.1 | 0.7 | 1.2 | 0.0011 | |||||
| 2.15 | Klei, zwak zandig, grijs, niet organisch, slap, kalkloos |
6.3 | 0.5 | 0.035 | 3.8 | 0.0003 | ||
| 11.8 | 0.4 | 23.3 | 0.0005 | |||||
| 23.9 | 0.5 | 23.5 | 0.0009 | |||||
| 48.1 | 0.5 | 10.8 | 0.0022 | |||||
| 96.1 | 0.5 | 6.2 | 0.0035 | |||||
| 3.45 | Klei, sterk zandig, grijs, niet organisch, slap, kalkloos | 6.8 | 0.4 | 0.023 | 8.2 | 0.0003 | ||
| 13.9 | 0.4 | 26.5 | 0.0005 | |||||
| 28.2 | 0.4 | 35.0 | 0.0008 | |||||
| 56.2 | 0.4 | 165.0 | 0.0014 | |||||
| 112.2 | 0.4 | 31.9 | 0.0024 |
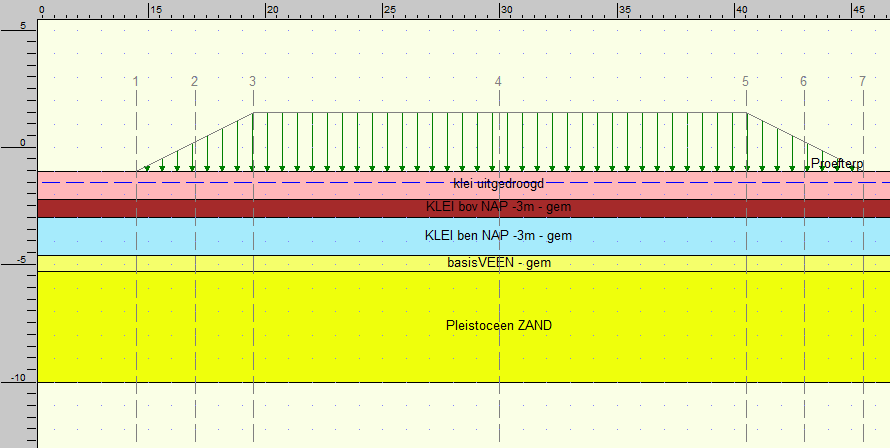
In parallel met de berekeningen met het CRACA-model zijn zettingsberekeningen uitgevoerd met het Koppejan model in D-Settlement. Gezien de vroege status van het project zullen deze beknopt worden gepresenteerd aangezien de berekeningen nog niet definitief zijn.. De geschematiseerde geometrie is weergegeven in Figuur 6. De parameters gebruikt in D-Settlement zijn weergegeven in Tabel 2.
Tabel 2; parameters gebruikt in D-Settlement
| Diepte bk laag | Laag | Cp/Cp’ | Cs/Cs’ | Cv |
| [m] NAP | [-] | [-] | [-] | [m2/jaar] |
| -1.0 | 1 | 12.4/3.1 | 93.8/23.5 | 3.2 |
| -2.2 | 2 | 10/2.5 | 63.6/15.9 | 3.2 |
| -3.0 | 3 | 5.6/1.4 | 32.5/8.1 | 3.2 |
| -4.6 | 4 | 2.5/0.6 | 14.4/3.6 | 6.3 |
| -5.3 | 5 (vaste zand) | n.v.t. | n.v.t. | n.v.t. |
Figuur 6; geometrie in D-Settlement
CONCLUSIE EN DISCUSSIE
Het CRACA model (Doherty & Bransby, 2019) is gebruikt voor het bepalen van de zetting van een proefterp welke is aangelegd ter ondersteuning van het bouwrijp maken van een terrein. Voor de berekeningen waren 3 boringen beschikbaar met in totaal 11 samendrukkingsproeven. De samendrukkingsproeven zijn direct in CRACA geladen waarmee vervolgens de zetting ten gevolge van een belastingverhoging van 45 kPa. De berekende zetting is weergegeven in Tabel 3. Door het directe gebruik van de meetdata van de samendrukkingsproeven is het afleiden van modelparameters niet nodig waardoor subjectiviteit door de gebruiker wordt geminimaliseerd.
De berekende zetting met het CRACA-model is vergeleken met een modellering in D-Settlement en het Koppejan model. De berekende waarden laten vergelijkbare te verwachten zettingen zien, hoewel de schematisering en modellering sterk verschillend is. Het Koppejan model lijkt hierbij grotere zettingen te voorspellen mede door de lagere consolidatiecoëfficiënten waardoor na 1 jaar nog geen volledige consolidatie is opgetreden. Hetgeen bij de consolidatiecoëfficiënten afgeleid met het CRACA model wel het geval is.
Tabel 3 berekende zetting na 1 jaar met het CRACA model in Koppejan model in D-Settlement.
| Settlement CRACA | Koppejan model |
| [m] | [m] |
| 0.36 (B13) | 0.36 |
| 0.24 (B14 | |
| 0.17 (B03 |
De meetdata van de proefterpen moet nog worden verwerkt en deze zal het mogelijk maken om een betere evaluatie van de uitgevoerde berekeningen te geven. Op basis van de uitgevoerde berekeningen met het CRACA-model lijkt dit een waardevolle toevoeging aan de beschikbare modellen om zettingen te berekenen. Het CRACA-model gebruikt de volledige dataserie die wordt verkregen wordt met samendrukkingsproeven en is niet afhankelijk van de beperkingen van een schematisering om de meetdata te beschrijven en de fouten die hierbij kunnen ontstaan. Toepassing van het CRACA-model vereist een groter aantal samendrukkingsproeven om een grondprofiel goed op basis van meetdata te kunnen beschrijven hetgeen zowel als een voordeel als nadeel kan worden gezien.
BRONVERMELDING
Doherty, J. P., & Bransby, F. M. (2019). A data-driven approach for predicting the time-dependent settlement of embankments on soft soil. Geotechnique.
Hoefsloot, F. (2015). Evaluation Settlement models Test Embankments Bloemendalerpolder – GeoImpuls Program. Geotechnical Safety and Risk V (pp. 628 – 633). IOS PRess. Retrieved from https://ebooks.iospress.nl/publication/42340
Houkes, B. C. (2016). Review and validation of settlement prediction methods for organic soft soils, on the basis three case studies from the Netherlands. TU Delft.
Kelly, R. B., Sloan, S. W., Pineda, J. A., Kouretzis, G., & Huang, J. (2018). Outcomes of the Newcastle symposium for the prediction of embankment behaviour on soft soil. Computers and Geotechnics, 93, 9-41. doi:https://doi.org/10.1016/j.compgeo.2017.08.005